Category: Scheme

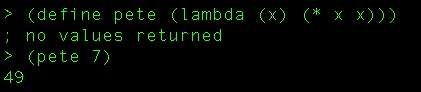
The last two posts just covered a basic overview of how Scheme’s syntax works and was kind of a way to just expose people to the language. This post is going to cover how you can use recursion in Scheme.

There are two very common mathematical examples that are always used when talking about recursion in programming. The first is computing a Factorial and the other is the Fibonacci sequence. Who am I to buck tradition?

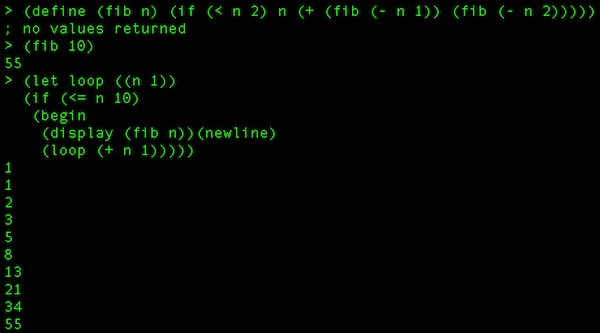
First, we’ll look at the Fibonacci sequence. The first 10 numbers of the sequence are 1 1 2 3 5 8 13 21 34 55.

Here is how we would implement that in Scheme.

(define (fib n) 
    (if (< n 2) 
     n 
     (+ (fib (- n 1))(fib (- n 2)))
    )
)

That function calls itself recursively to figure out what the nth digit of the Fibonacci sequence is. So, if we'd like to see it print out in a chain, we can just call that function in a loop.

(let loop ((n 1))
  (if (<= n 10)
    (begin
     (display (fib n))(newline)
     (loop (+ n 1))
    )
  )
)

That looks like this:

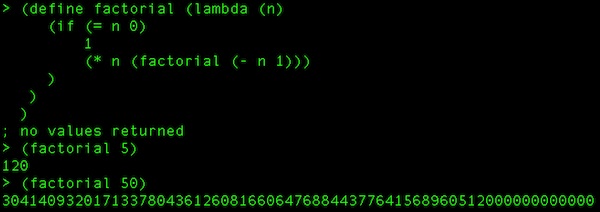
A factorial (ex: 5! = 5 * 4 * 3 * 2 * 1 = 120) in Scheme would be coded simply like this:

(define factorial 
  (lambda (n) 
     (if (= n 0)  
         1
         (* n (factorial (- n 1)))
     )
   )
 )

Here is something interesting. Because Scheme is dynamic with its type system and this function can return anything, I can actually work with really large numbers. For example, here I call the function twice, once with 5 to return 120 and the second time with 50 to return 30414093201713378043612608166064768844377641568960512000000000000. That is obviously WAY too big to be returned with any native .Net data type. Also, both of those calls returned as quickly as I hit Enter.

Up until now, there isn't much special about these recursive functions. However, Scheme does allow something that C# doesn't allow (well, it can in very special circumstances) and that is tail recursion. This is also (sometimes controversially) called tail optimization and is something of a hallmark of functional languages.

Traditionally, for every method/function/procedure call you are making in a language, you are building on the stack until that method/function/procedure returns. You see this all the time when you look at a stack trace while you are debugging. However, when you recursively call the same method over and over and over again, you risk a stack overflow. Imagine I wanted to find out what 50000! was. I would be putting 50000 function calls (all to the same function) on the stack and depending on the architecture I was on, I could overflow the stack (on my Macbook Pro, it did return after a few minutes with a VERY large number - pages and pages of scrolling).

What tail call optimization does is "discard" the stack up to the point when it calls itself again because the function will just be returning itself, so it doesn't need to keep track. If that sounds wayyy insane, let's think about our terms. First "tail position" refers to the last thing that happens in a function before it returns. In the case of tail recursion, the last thing that occurs is a call to the function itself. Even though it looks like my factorial example from earlier might be tail recursive, it really isn't. Here it is again.

(define factorial 
  (lambda (n) 
     (if (= n 0)  
         1
         (* n (factorial (- n 1)))
     )
   )
 )

Take notice of the last line: (* n (factorial (- n 1))). You see how the last thing the function does is multiply the number passed in (n) against the result of the function called again with "n minus 1". So, we can't just jump ahead to the new function and only return its results because those need to bubble up the stack, being multiplied against the function's original n all the way up.

What we need to do is track our own progress, so that the function doesn't need to be multiplied by anything outside of itself. One thing we could do is just take the accumulation as a second parameter, but that is relying on the caller of the function to kind of do something unnatural and not obvious when calling the function. What we'll do instead is declare a local function inside of our function and call this local function with our parameter and a variable that accumulates and tracks our state.

The factorial function in full tail-recursive glory could look something like this

(please note: this isn't formatted the "Scheme-Way" because I was trying to make it as readable as possible)

(define pete_factorial ; our function
 (letrec ; defining something here with local scope
  (
   (inner_factorial ; a locally scoped function 
    ; local function is a lambda taking 2 params
    (lambda (the_number our_accumulator) 
     (if (= the_number 0) ; if the number passed in is 0
       ; return the current accumulation
       our_accumulator
       ; else call the local function again with the decremented 
       ;number and an up-to-date accumulator
       (inner_factorial (- the_number 1) (* our_accumulator the_number)) 
     ) ;closing the if
    ) ; closing the lambda
   ) ; closing the inner function def
  ) ; closing the letrec body
; actual pete_factorial definition is a lambda
(lambda (actual_parameter_passed_in_to_pete_factorial) 
  ; lambda body that calls the local function with the param and 
  ; an initial accumulator of 1
  (inner_factorial actual_parameter_passed_in_to_pete_factorial 1) 
) ; close lambda
) ; close pete_factorial body
) ; close define statement

Hopefully, that is fairly clear. I've actually had this post in the hopper for some time while I wrapped my head around exactly what we were accomplishing here. Then, when I thought I had it and it was time to write, I still wasn't prepared to explain it clearly. I hope that the combination of the formatting, comments, and verbose variable names helps you to understand it. I know that it helped me out a great deal.

As I've said, our basic goal here is to keep the stack from having to keep track of our state. In the original one, it worked out to be something like

factorial(5)
5*factorial(4)
5*4*factorial(3)
5*4*3*factorial(2)
5*4*3*2*factorial(1)
5*4*3*2*1*factorial(0)
5*4*3*2*1*1
120

In my severely-commented tail recursive case, it doesn't have to do that. It loads the function onto the stack and it keeps it there. Every definition describes that it basically does a GOTO and just keeps calling back to the top of the function (the inner function) over and over again. Because we keep our own state, the last thing to evaluate is just returned because the last value of the function is the answer.

This time, it is:

(pete_factorial 5)
replace arguments with (5 1), goto "inner_factorial"
replace arguments with (4 5), goto "inner_factorial"
replace arguments with (3 20), goto "inner_factorial"
replace arguments with (2 60), goto "inner_factorial"
replace arguments with (1 120), goto "inner_factorial"
replace arguments with (0 120), goto "inner_factorial"
return 120

I know we've covered a lot here, but this is good solid computer science stuff. It definitely doesn't hurt to think about it from time to time and really understand what is going on with the computer and within our languages when we write our code.

If you have any questions, or want me to try to clarify something, let me know in the comments and I'll do the best I can.

In my last post, I started to look at the Scheme language. We finished up with a simple if statement. Its syntax is like this: (if (condition) result1 result2).

In our last example, “result1” and “result2” were simple return types. If you wanted, the “result1” or “result2” could also be functions that are evaluated to get a return value. Let’s look at that.

In this case, if 4 is greater than 0, we are going to multiply 4 times 4, if 4 isn’t greater than 0, we are just going to add 4 plus 4.

(if (> 4 0) (* 4 4) (+ 4 4))

You can see that because 4 is greater than 0, it executed the first block which evaluated 4 * 4 which is 16. Like last time, here is the equivalent C# version to hopefully add clarity.

if (4 > 0)
{
     return 4 * 4;
}
else
{
     return 4 + 4;
}

One of the most powerful things you can do in a functional language is – of course – to define your own functions. Here is a simple function that defines a function named pete that squares a number passed to it.

(define pete (lambda (x) (* x x)))

So here, we are calling the define language construct (which is how you declare variables, functions, etc in Scheme) and defining “pete” which is a lambda that takes one parameter – x – and returns the output of the * function being passed x and x. You see that if we call the pete function and pass in 7, it returns 49 as you would expect.

Functions are first class citizens in Scheme, so you can pass them around as arguments. Let’s see this example where I’m going to let us “do-stuff-to-four-and-nine”. My goal here is that we are going to create a function that takes a function as a parameter. It then calls that function, passing it 4 and 9.

So, first the function. (I used a hard return in the REPL window so that the screenshot below would definitely fit. It does not cause a problem in the language to have it there).

(define do-stuff-to-four-and-nine (lambda (our-func) (our-func 4 9)))

All I’ve done is define “do-stuff-to-four-and-nine” as a function that takes a parameter (our-func) that I then use in the body of the lambda, calling it and passing 4 and 9 as arguments. Next, let’s define 4 functions that we can pass to our “do stuff” function.

You should be able to simply read these by now. All four take two parameters, and are plainly named for the simple operations they perform on them.

Now, all that is left is to call the “do-stuff” function and pass it each of these functions in turn.

Interestingly, the function must take the right number of arguments. If not, the language throws up on you. Notice here that I define a function that only takes one argument. Then when I try to pass it in to our “four and nine” function, I get an error.

I hope that you’ve learned a little bit more about how Scheme works and how powerful it can be. My next post is going to take a look at recursion in Scheme and putting a lot of these lessons together.

The other night, I was reading through Hacker News or Programming Reddit or something and I found an article about writing compilers that supposedly simplified it enough that it could be taught to beginner-level computer science students. It uses potentially hundreds of complier passes to make simple transforms to the code until it has completed its task.

I thought that I’d check it out and I saw that it was written in Scheme. I personally hadn’t spent any time in LISP or any LISP dialects, so it seemed like something interesting to dive in to.

On my Mac, using Homebrew, it was a breeze to get started. At first, I just typed

brew search scheme

I found what I was looking for and then typed

brew install scheme48

Here is an example of what you would see installing it on a Mac.

That’s it! (if you are on Windows, you can get install instructions here)

The only things I knew about Scheme were that it was functional and there were a lot of parentheses. I was right on both accounts. Aside from a few exercises where you were to type a number and have it spit back out to you, the first thing you run into is this:

(* 2 2)

Well, at first glance, stuff like that will throw you a little bit. However, with only a little bit of thought, you can see that it makes perfect sense. We have to think functionally. The parentheses tell us that this group is all one function call and reading left to right we see that we are calling the multiplication function – the * – and passing in the numbers 2 and 2 as arguments. That’s it. So (* 2 2) outputs 4 and (* 2 3 4) outputs 24. Also, we need the parentheses. Without them, you don’t get the desired result as you can see below.

What about control flow? That, too, is very simple. The syntax is simply (if (condition) result1 result2). It is very similar to an IIF statement, but without the commas. If you take this code, you get the result pictured below.

(if (< 4 5) "four is less than 5" "four is not less than five")

If you are having any trouble making sense of it, it might be helpful to think of this code in terms of how it breaks out in C#

if (4 < 5)
{
     return "four is less than five";
}
else
{
     return "four is not less than five";
}

I hope that if the Scheme code was confusing to you, that the C# translation helped a bit. You'll notice that just as a Ruby function returns the last thing that was evaluated, so too does Scheme. That's why there are no return statements in my Scheme example, but there are in the C# example.

Next time, we'll look at more complex if statements and travel down the functional road a little further.